Недорого купить диплом бакалавра любого ВУЗа страны

Министерство образования Российской Федерации. Московский государственный институт электроники и математики

Название	Министерство образования Российской Федерации. Московский государственный институт электроники и математики
	Кириллов Т.А
Дата конвертации	09.11.2013
Размер	75.56 Kb.
Тип	Документы
источник

Министерство образования Российской Федерации.

Московский государственный институт электроники и математики

(технический университет).

Расчетно-графическая работа №1

на тему «Постоянный ток».

Вариант 6.

Выполнил:

студент группы С35

Кириллов Т.А.

Проверил:

преподаватель

Рябов Н.И.

Москва – 2009.

Значения параметров:

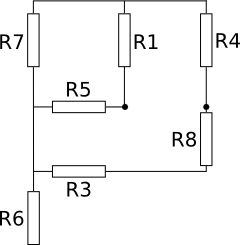
R1	R2	R3	R4	R5	R6	R7	R8	E1	E2	E3	E4	E5	E6	J	I1
3	4	4	5	6	7	8	2	?	20	30	40	50	20	2	1

Схема:

Задание 1.

Написать по законам Кирхгофа систему уравнений для определения неизвестных токов и э.д.с. в ветвях схемы (решать эту систему уравнений не следует).

Первый закон Кирхгофа:

I7 = I1 + I4;

I4 + I8 = J + I2;

J + I3 = I8;

I1 + I2 = I5;

Второй закон Кирхгофа:

I7 * R7 + I1 * R1 + I5 * R5 = E1 + E5;

I1 * R1 - I2 * R2 - I4 * R4 = E1 - E2 - E4;

I3 * R3 + I8 * R8 + I2 * R2 + I5 * R5 = E3 + E2 + E5;

I8 * R8 = U_J;

Задание 2.

Определить неизвестные токи и э.д.с. в ветвях схемы методом контурных токов.

Ik1 * (R7 + R1 + R5) + Ik2 * R5 + Ik3 * R7 = E1 + E5;

Ik2 * (R5 + R2 + R3 + R8) + Ik1 * R5 - Ik3 * (R3 + R8) = E2 + E3 + E5 -J * R8;

Ik3 * (R7 + R3 + R8 + R4) + Ik1 * R7 - Ik2 * (R3 + R8) = E4 - E3 + J * R8;

Добавим уравнение для разрешения системы:

I1 = Ik1;

Преобразуем к виду:

Ik2 * R5 + Ik3 * R7 - E1 = E5 - I1 * (R1 + R5 + R7);

Ik2 * (R2 + R3 + R5 + R8) - Ik3 * (R3 + R8) + 0 * E1 = E2 + E3 + E5 - J * R8 - I1 * R5;

-Ik2 * (R3 + R8) + Ik3 * (R3 + R4 + R7 + R8) + 0 * E1 = E4 - E3 + J * R8- I1 * R7;

Составим матрицу системы:

6	8	-1	16
16	-6	0	86
-6	19	0	-4

Решение:

Ik2 = 6.0075 (А);

Ik3 = 1.6866 (А);

E1 = 33.5373 (В);

Найдем токи в ветвях:

I2 = Ik2 = 6.0075 (А);

I3 = Ik2 - Ik3 = 4.3209 (А);

I4 = Ik3 = 1.6866 (А);

I5 = Ik1 + Ik2 = 8.0075 (А);

I7 = Ik1 + Ik3 = 3.6866 (А);

I8 = Ik2 - Ik3 + J = 5.3209 (А);

Задание 3.

Составить баланс мощностей для исходной схемы.

P_{активн.} = I5 * E5 + I1 * E1 + I2 * E2 + I4 * E4 + I3 * E3 + (I8 * R8) * J = 795.3;

P_{пассивн.} = I1² * R1 + I2² * R2 + I3² * R3 + I4² * R4 + I5² * R5 + I7² * R7 + I8² * R8 = 795.3;

Задание 4.

Определить напряжение измеряемое вольтметром.

Uv1 = E6 + E3 - I3 * R3 = 32.716 (В);

Uv2 = E3 + E5 - I5 * R5 - I3 * R3 = 14.671 (В);

Задание 5.

Методом эквивалентного источника напряжения определить ток во второй ветви, а также найти величину и направление э.д.с., которую надо дополнительно включать в эту ветвь, чтобы ток на ней увеличился в 2 раза и изменил свое направление.

Определяем Eэкв .

Считаем проводимость в нужных ветвях:

g11 = 1 / R1 + 1 / R7 + 1 / R4 = 0.65833 (см);

g12 = 1 / R4 = 0.2 (см);

g13 = 1 / R7 = 0.125 (см);

g14 = 1 / R1 = 0.33 (см);

g22 = 1 / R4 + 1 / R8 = 0.7 (см);

g25 = 1 / R8 = 0.5 (см);

g33 = 1 / R3 + 1 / R5 + 1 / R7 + 1 / R6 = 0.684 (см);

g34 = 1 / R5 = 0.167 (см);

g35 = 1 / R3 = 0.25 (см);

g44 = 1 / R1 + 1 / R5 = 0.5 (см);

g55 = 1 / R3 + 1 / R8 = 0.75 (см);

По методу узловых потенциалов:

Ф1 * g11 - Ф2 * g12 - Ф3 * g13 - Ф4 * g14 = - E1 * g1 - E4 * g4;

- Ф1 * g12 + Ф2 * g22 - Ф5 * g25 = - J + E4 * g4;

- Ф1 * g13 + Ф3 * g33 - Ф4 * g34 - Ф5 * g35 = E6 * g6 + E5 * g5 - E3 * g3;

- Ф1 * g14 - Ф3 * g34 + Ф4 * g44 = E1 * g1 - E5 * g5;

- Ф2 * g25 - Ф3 * g35 + Ф5 * g55 = E3 * g3 + J;

Потенциал Ф5 возьмем равным 0, тогда имеем систему:

Ф1 * g11 - Ф2 * g12 - Ф3 * g13 - Ф4 * g14 = - E1 * g1 - E4 * g4;
- Ф1 * g12 + Ф2 * g22 = - J + E4 * g4;

- Ф2 * g25 - Ф3 * g35 = E3 * g3 + J;

- Ф1 * g14 - Ф3 * g34 + Ф4 * g44 = E1 * g1 - E5 * g5;

Матрица системы:

0.65833	-0.2	-0.125	-0.33	-19.1791
-0.2	0.7	0	0	6
0	-0.5	-0.25	0	9.5
-0.33	0	-0.167	0.5	2.8458

Решение:

Ф1 = -55.6297 (В);

Ф2 = -7.3228 (В);

Ф3 = -23.3545 (В);

Ф4 = -39.1797 (В);

Тогда Eэкв = Ф2 - Ф4 = 31.857 (В);

Определяем Rэкв .

Преобразуем треугольник R7 – R5 – R1 в звезду R7a – R5a – R1a: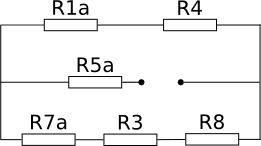

R5a = R5 * R1 / (R1 + R5 + R7) = 1.059 (Ом);

R7a = R7 * R5 / (R1 + R5 + R7) = 2.824 (Ом);

R1a = R1 * R7 / (R1 + R5 + R7) = 1.412 (Ом);

R1a4 = R1a + R4 = 6.412 (Ом);

R7a38 = R7a + R3 + R8 = 8.824 (Ом);

Rэкв = R5a + R1a7a438 = R5a + R1a4 * R7a38 / (R1a4 + R7a38) = 4.772 (Ом);

I2 = (Eэкв + E2) / (Rэкв + R2) = 6 (А);

Найдем величину и направление э.д.с., которую надо дополнительно включить во вторую ветвь, чтобы ток в ней увеличился в 2 раза и изменил свое направление.

- 2 * I2 * (Rэкв + R2) = Eэкв + E2 - E;

E = 157 (В);

E сонаправлена с E2.

Добавить документ в свой блог или на сайт

Похожие:

	Министерство общего и профессионального образования российской федерации московский государственный институт электроники и математики (Технический университет) Московский государственный институт электроники и математики (Технический университет)		Министерство Образования Российской Федерации Московский Государственный Институт Электроники и Математики
	Министерство образования и науки РФ московский государственный институт электроники и математики Программирование в операционной среде unix на командном языке «shell» /Московский государственный институт электроники и математики;...		Министерство образования и науки российской федерации московский государственный институт электроники и математики (технический университет)
	Министерство образования и науки российской федерации московский государственный институт электроники и математики (технический университет)		Министерство образования Российской Федерации Московский Государственный Институт Электроники и Математики Кафедра электронно-вычислительной аппаратуры объектно-ориентированные субд
	Министерство образования Российской Федерации Московский Государственный Институт Электроники и Математики Кафедра электронно-вычислительной аппаратуры объектно-ориентированные субд		Министерство образования российской федерации московский государственный институт электроники и математики Проверить по правилу «3 сигма», что выборка получена из заданного закона распределения
	Министерство образования Российской Федерации. Московский государственный институт электроники и математики В момент времени t = 0 коммутирует рубильник 1, а через промежуток t1 – рубильник 2		Министерство общего и профессионального образования российской федерации московский государственный институт электроники и математики Алгоритмы синтеза абстрактного автомата на примере четырехразрядного сумматора двоичных чисел
	Министерство образования и науки российской федерации московский государственный институт электроники и математики Изучить и описать правила оформления документации на предприятии (в том числе нормативные документы)

Разместите кнопку на своём сайте:
Документы

База данных защищена авторским правом ©textedu.ru 2000-2013
При копировании материала обязательно указание активной ссылки открытой для индексации.