Недорого купить диплом бакалавра любого ВУЗа страны Расчетно-графическая работа Пример. Расчет переходных процессов операторным методом
Реклама: | Скачать 10.89 Kb.
|
| Расчетно-графическая работа 2. Пример. Расчет переходных процессов операторным методом. 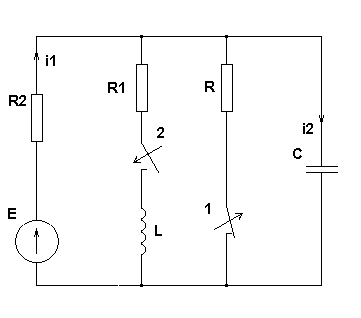 Первая коммутация. Независимое начальное условие - напряжение на емкости перед первой коммутацией:  Операторная эквивалентная схема: 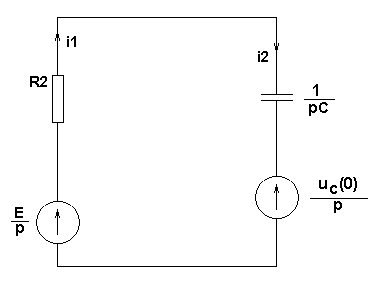 Вычислим изображение по Лапласу тока i1, равного i2: 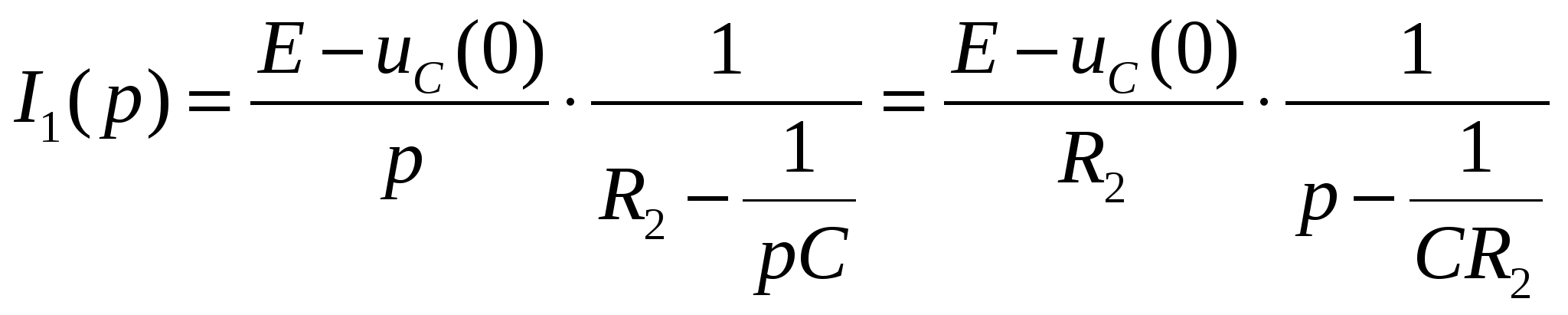 Проведя обратное преобразование Лапласа с помощью таблиц, получим: 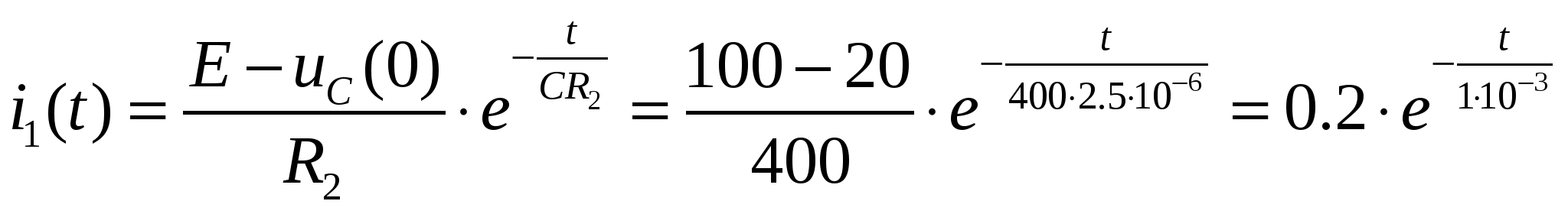 Вторая коммутация. Независимые начальные условия вычислены ранее:  Операторная эквивалентная схема: 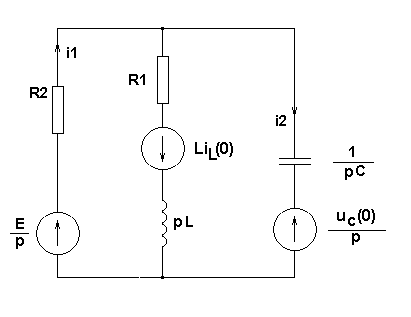 Найдем изображение по Лапласу тока i2 методом наложения:  ,где: ток I2E(p) обусловлен источником эдс E, а I2E(p) - перезарядкой емкости C, ток индуктивности в начальный момент времени равен нулю. 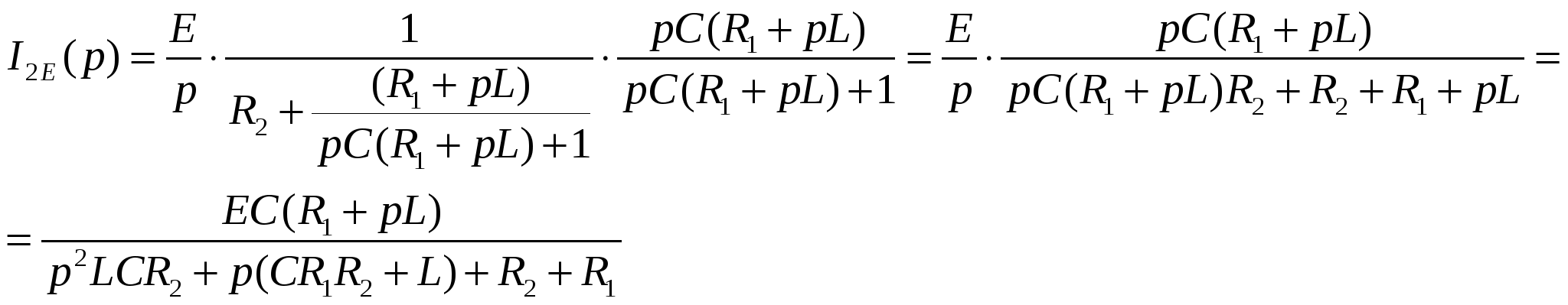   Ищем корни знаменателя: 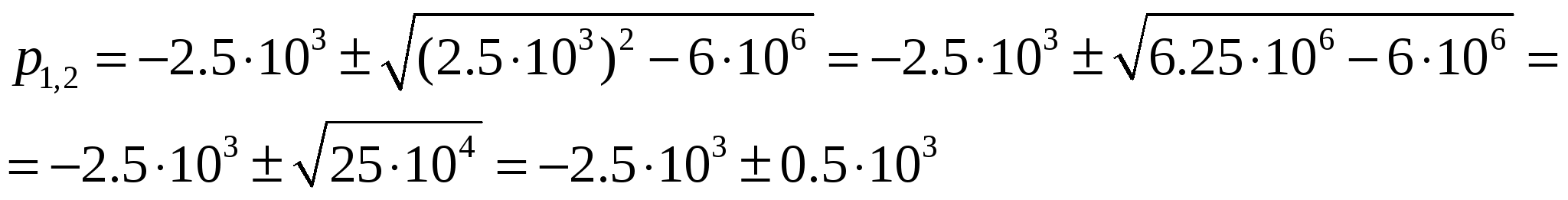  .Ищем оригинал с помощью теоремы разложения:    |
Добавить документ в свой блог или на сайт
Реклама:
Похожие:
 | Целью работы является приобретение навыков экспериментального исследования переходных процессов с помощью электронно-лучевого осциллографа,... | | Целью работы является приобретение навыков экспериментального исследования переходных процессов с помощью электронно-лучевого осциллографа,... |
| Целью работы является приобретение навыков экспериментального исследования переходных процессов с помощью электронно-лучевого осциллографа,... | | Расчетно-графическая работа по дисциплине «Теория вероятности и математическая статистика» |
| В работе выполняется расчёт оптимальных маршрутов сети при помощи алгоритма Беллмана-Форда и Дейкстры | | В работе выполняется расчёт оптимальных маршрутов сети при помощи алгоритма Беллмана-Форда и Дейкстры |
| В работе выполняется расчёт оптимальных маршрутов сети при помощи алгоритма Беллмана-Форда и Дейкстры | | В работе выполняется расчёт оптимальных маршрутов сети при помощи алгоритма Беллмана-Форда и Дейкстры |
| Смоделировать выборку из равномерного закона распределения с параметрами a=0,12 и b =3,51 (R[0,12; 3,51]) | | Смоделировать выборку из равномерного закона распределения с параметрами a=-1,3 и b =2,4 ( R[-1,3;2,4] ) |